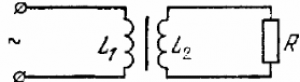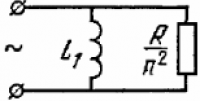Найти ЭДС генератора в виде квадратной рамки, вращающейся в постоянном магнитном поле.

$$ {\cal E}=-\frac{d\Phi}{dt}=-\frac{d\left(\vec{B}\cdot\vec{S}\right)}{dt}=-\frac{d\left(BS\cos\left(\omega t\right)\right)}{dt}=BS\omega\sin\left(\omega t\right). $$

На один сердечник намотаны две катушки с коэффициентами самоиндукции $L_1$ Гн и $L_2$. Чему равен коэффициент взаимоиндукции? Рассеяния магнитного поля нет.

Пусть в сердечнике поток \(\Phi _0\). Потокосцепление в первой катушке \[ \Phi _1 = N_1 \Phi _0 = {L_{11} I_1 + L_{12} I_2 }, \] и во второй катушке \[ \Phi _2 = N_2 \Phi _0 = {L_{22} I_2 + L_{21} I_1 } . \] Пустим в первой катушке ток \(I_1\) а во второй ток занулим. Тогда \[ \frac{{L_{11} }}{{L_{21} }} = \frac{{N_1 }}{{N_2 }}. \]

Теперь пустим ток через 2 катушку, а первую разомкнем. Тогда \[ \frac{{L_{12} }}{{L_{22} }} = \frac{{N_1 }}{{N_2 }}. \] Разделив друг на друга два последних соотношения, получим \[ \sqrt{L_{12}L_{21}} = \sqrt {L_1 L_2 }, \] и, используя соотношение \(M= L_{12}=L_{21}\), получаем для коэффициента взаимоиндукции \[ M=\sqrt{L_{12}L_{21}}=\sqrt{L_{1}L_{2}}. \]

К вторичной обмотке трансформатора подключено сопротивление $R$, к первичной — генератор синусоидального напряжения. Найти ток в первичной обмотке, если коэффициенты самоиндукции обмоток $L_1$ и $L_2.$ Потоками рассеяния и сопротивлениями обмоток пренебречь.

Запишем уравнения для контуров $$ {\cal E}+{\cal E}_{11}+{\cal E}_{21}=0, \ \ {\cal E}_{12}+{\cal E}_{22}=RI_{2} $$ Величины ЭДС $$ {\cal E}_{11}=-L_{1}\dot{I}_{1}, \ \ {\cal E}_{12}=-M\dot{I}_{1}, \ \ {\cal E}_{21}=-M\dot{I}_{2}, \ \ {\cal E}_{22}=-L_{2}\dot{I}_{2} $$

Так как $I_{k}\sim I_{0k}e^{i\omega t},$ то $\dot{I}_{1}=i\omega I_{1}$ тогда

$$ {\cal E}=i\omega\left(L_{1}I_{1}+MI_{2}\right), \ \ -i\omega\left(MI_{1}+L_{2}I_{2}\right)=RI_{2}. $$ $$ I_{2}=-I_{1}\frac{i\omega M}{i\omega L_{2}+R}. $$ $$ {\cal E}=i\omega I_{1}\left(L_{1}-\frac{i\omega M^{2}}{i\omega L_{2}+R}\right) =iI_{1}\omega\left(L_{1}-\frac{i\omega M^{2}}{i\omega L_{2}+R}\right)= $$ $$ iI_{1}\omega\left(L_{1}-\frac{i\omega M^{2}}{i\omega L_{2}+R}\right)= iI_{1}\omega\left(\frac{L_{1}\left(i\omega L_{2}+R\right)-i\omega\left(L_{1}L_{2}\right)}{i\omega L_{2}+R}\right)\approx $$ $$ I_{1}\left(\frac{i\omega L_{1}R}{i\omega L_{2}+R}\right). $$

$$ Z=\frac{i\omega L_{1}R}{i\omega L_{2}+R} \cdot\frac{\frac{L_{1}}{L_{2}}}{\frac{L_{1}}{L_{2}}}= \frac{i\omega L_{1}\cdot R\frac{L_{1}}{L_{2}}}{i\omega L_{1}+R\frac{L_{1}}{L_{2}}}= $$ $$ \left(\frac{1}{i\omega L_{1}}+\frac{1}{R\frac{L_{1}}{L_{2}}}\right)^{-1}= \left(\frac{1}{Z_{L}}+\frac{1}{R\frac{L_{1}}{L_{2}}}\right)^{-1}. $$ $$ \frac{L_{1}}{L_{2}}=\frac{L_{1}}{L_{2}} \cdot\frac{L_{1}}{L_{1}}= \frac{L_{1}^{2}}{L_{12}^{2}}= \frac{N_{1}^{2}}{N_{2}^{2}}= \frac{1}{n^{2}}. $$

Рассчитать глубину скин–слоя для меди, железа и алюминия.

Система уравнений Максвелла и материальные уравнения среды в СИ имеют вид $$\text{rot}\,\vec{E}=-\frac{\partial\vec{B}}{\partial t}\,,\ \ \text{div}\,\vec{D}=\rho , $$ $$\text{rot}\,\vec{H}=j+\frac{\partial\vec{D}}{\partial t}\,,\ \ \text{div}\,\vec{B}=0, $$ Поскольку плотность токов смещения $\frac{\partial\vec{E}}{\partial t}$ в проводящей среде мала по сравнению с током проводимости $j=\sigma E$, то уравнения принимают вид $$\text{rot}\,\vec{E}=-\frac{\partial\vec{B}}{\partial t} = -\mu \mu_0\frac{\partial\vec{H}}{\partial t} \,, \ \ \text{rot}\,\vec{H}=\sigma\,\vec{E}\,.$$ Используя эти уравнения, можно получить дифференциальное уравнение, содержащее только вектор напряженности электрического или магнитного полей.

\begin{equation*} -\text{rot}\,\text{rot}\, \vec{E} = \nabla^2\vec{E}-\text{div}\vec{E} = \nabla^2\vec{E}= \mu\mu_0 \sigma\;\frac{\partial\vec{E}}{\partial t}\,. \end{equation*} Электрическое поле в проводнике у его поверхности равно $\;\vec{E}=\vec{E_0}\,\exp (-i\omega\,t)$. В переменном поле с частотой $\;\omega$ зависимость всех величин от времени описывается множителем $\;\exp(-i\omega\,t)$. Тогда уравнение в одномерном случае примет вид $$\frac{\partial^2\vec{E}}{\partial z^2}+ k^2\vec{E}=0\,, $$ где с учётом $(1-i)^2=1-2i+i^2=-2i$ $$k=\sqrt{-i\,\mu\mu_0 \sigma\omega}= \pm\sqrt{\frac 12\mu\mu_0 \sigma\omega} \cdot (1-i)= \pm\frac{1-i}{\delta}\,,\quad \delta=\sqrt{\frac 2{\mu\mu_0 \sigma\omega}}\,.$$ Решение этого уравнения, обращающееся в нуль при $\;z \to\infty$. Учитывая граничное условие при $\,z=0$, получаем $$\vec{E}=\vec{E_0}\,e^{\textstyle-\frac{z}{\delta}}\, e^{\textstyle-i(\omega\,t-\frac{z}{\delta})}.$$

Найти среднюю за период мощность, выделяющуюся в бесконечно глубоком столбике единичной площади.