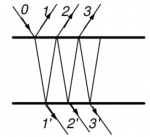
Временная и пространственная когерентность. Контрастность.
Немонохроматический источник в схеме Ллойда.
 Рассчитать видность для немонохроматического источника в схеме с зеркалом Ллойда.
Рассчитать видность для немонохроматического источника в схеме с зеркалом Ллойда.
Помним, что в схеме Ллойда к набегу разности фаз при прохождении по двум разным путям $\Delta\varphi =k(l_{2}-l_{1})$ вызванному разницей расстояний $l_{2}-l_{1}=\frac{2xh}{L}$ добавится ещё скачок на $\pi$, связанный с отражением от зеркала. Так, что интенсивность
$$I=2I_{0}\left(1+\cos\left(\Delta\varphi+\pi\right)\right)=2I_{0}\left(1-\cos k\frac{2xh}{L}\right).$$
Если источник монохроматичен, то видность $$V=\frac{I_{max}-I_{min}}{I_{max}+I_{min}}=1,$$ так как $I_{max}=4I_{0},\,I_{min}=0.$
Учтём теперь, что источник немонохроматичен и его волновой вектор меняется в пределах $k$ так, что $k\pm \frac 12 \Delta k$.
Если, например, сложить две немонохроматичные волны, то итоговая интенсивность двух волн:
$$ I\sim EE^{*}=\left(E_{1}e^{i\omega_{1}t}+E_{2}e^{i\omega_{2}t}\right)\left(E_{1}e^{-i\omega_{1}t}+E_{2}e^{-i\omega_{2}t}\right)= $$ $$ E_{1}^{2}+E_{2}^{2}+E_{1}E_{2}\left(e^{i\left(\omega_{1}-\omega_{2}\right)t}+e^{i\left(\omega_{2}-\omega_{1}\right)t}\right)= $$ $$ E_{1}^{2}+E_{2}^{2}+2E_{1}E_{2}\cos\left(\left(\omega_{1}-\omega_{2}\right)t\right). $$ и после усреднения по времени — переменное слагаемое уйдёт, так что $I=I_{1}+I_{2}$ т.е. итоговая интенсивность будет суммой интенсивностей двух монохроматичных источников.
Представим наш немонохроматичный источник в виде бесконечной суммы монохроматичных и сложим их интенсивности:
$$I=\intop_{k-\frac{1}{2}\Delta k}^{k+\frac{1}{2}\Delta k}dI={\displaystyle \intop_{k-\frac{1}{2}\Delta k}^{k+\frac{1}{2}\Delta k}}\frac{2I_{0}}{\Delta k}\left(1-\cos k\frac{2xh}{L}\right)dk= $$ $$\left.\frac{2I_{0}}{\Delta k}\left(k-\frac{L}{2xh}\sin k\frac{2xh}{L}\right)\right|_{k-\frac{1}{2}\Delta k}^{k+\frac{1}{2}\Delta k}= $$ $$ \frac{2I_{0}}{\Delta k}\left(\Delta k-\frac{L}{2xh}\sin\left(k+\frac{1}{2}\Delta k\right)\frac{2xh}{L}+\frac{L}{2xh}\sin\left(k-\frac{1}{2}\Delta k\right)\frac{2xh}{L}\right). $$ с учётом $$\sin\left(\alpha+\beta\right)=\sin\left(\alpha\right)\cos\left(\beta\right)+\sin\left(\beta\right)\cos\left(\alpha\right):$$
$$I=\frac{2I_{0}}{\Delta k}\left(\Delta k-\frac{L}{xh}\sin\frac{xh\Delta k}{L}\cos\frac{2xhk}{L}\right)=$$
$$ 2I_{0}\left(1-\frac{L}{\Delta kxh}\sin\frac{xh\Delta k}{L}\cos\frac{2xhk}{L}\right)=2I_{0}\left(1-\text{sinc}\frac{xh\Delta k}{L}\cos\frac{2xhk}{L}\right),$$
где $\text{sinc}\,u=\frac{\sin u}{u}$ — периодическая, затухающая функция.
Тогда видность $$V=|\text{sinc}\frac{xh\Delta k}{L}|$$ упадёт первый раз до нуля при $\frac{xh\Delta k}{L}=\pi$, но до единицы далее доходить уже не будет.
Линии равного наклона и равной толщины.
Коэффициент пропускания плоскопараллельной пластины
Принимая интенсивность падающего пучка за единицу, найти интенсивность проходящего и отраженного пучков при многократной интерференции на плоскопараллельной пластинке (поглощение света отсутствует).
Падает луч света интенсивностью $I_{0}$ и отражается от границы с энергетическим коэффициентом отражения $R.$ Тогда интенсивности прошедших лучей выразятся в виде
$$I_{1'}=\left(1-R\right)^{2}I_{0}$$ $$I_{2'}=R^{2}I_{1'}=R^{2}\left(1-R\right)^{2}I_{0}$$ $$I_{3'}=R^{2}I_{2'}=R^{4}\left(1-R\right)^{2}I_{0}$$
Получаем, что на $m+1$ шаге интенсивность
$$I_{m+1}=R^{2m}\left(1-R\right)^{2}I_{0}.$$
Амплитуда электрического поля $E\sim\sqrt{I}$ так, что
$$E_{m+1}=R^{m}\left(1-R\right)E_{0}$$
Но нам надо учесть, что разные волны после отражений будут проходить разные расстояния и, соответственно, будут иметь разные фазы. Найдём разность фаз между соседними волнами.
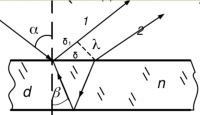
Оптическая длина первого луча, с учётом отражения от более плотной оптической среды: $$\ell_{1}=\frac{\lambda}{2}+\delta_{1},$$ где $\delta_{1}=\delta\sin\alpha,$ $\delta=2d\, \text{tg}\beta$
так, что
$$\ell_{1}=\frac{\lambda}{2}+2d\,\text{tg}\beta\sin\alpha.$$
Оптическая длина второго луча:
$$\ell_{2}=\frac{2nd}{\cos\beta}.$$
Учитывая закон Снелиуса найдём разность
$$\Delta=\ell_{2}-\ell_{1}=\frac{2nd}{\cos\beta}-2d\,\text{tg}\beta\sin\alpha-\frac{\lambda}{2}= $$
$$ \frac{2nd}{\cos\beta}-2dn\,\text{tg}\beta\sin\beta-\frac{\lambda}{2}=$$
$$\frac{2nd}{\cos\beta}\left(1-\sin^{2}\beta\right)-\frac{\lambda}{2}=2nd\cos\beta-\frac{\lambda}{2}$$
Если смотреть прошедшую волну, то отражения от раздела с более плотной оптической средой нет, значит нет и дополнительного набега фаз. Итак, разность хода между двумя соседними лучами $$\Delta=2nd\cos\beta,$$ тогда суммарная амплитуда прошедшей волны с учётом набега фазы $$\varphi=k\Delta=\frac{4\pi nd\cos\beta}{\lambda}:$$ $$ E={\displaystyle \sum_{m=0}^{\infty}E_{m+1}e^{im\varphi}=\left(1-R\right)E_{0}\sum_{m=0}^{\infty}e^{im\varphi}R^{m}}=\left(1-R\right)E_{0}\frac{1}{1-e^{i\varphi}R}$$
Найдём, теперь интенсивность прошедшей волны: $I\sim EE^{*}$
$$I_{D}=\left(1-R\right)^{2}I_{0}\frac{1}{\left(1-e^{i\varphi}R\right)\left(1-e^{-i\varphi}R\right)}=\frac{\left(1-R\right)^{2}I_{0}}{1+R^{2}-2R\cos\varphi}=$$
$$\frac{\left(1-R\right)^{2}I_{0}}{\left(1-R\right)^{2}+2R\left(1-\cos\varphi\right)}=\frac{\left(1-R\right)^{2}I_{0}}{\left(1-R\right)^{2}+4R\sin^{2}\frac{\varphi}{2}}=\frac{I_{0}}{1+R\left(\frac{2\sin\frac{\varphi}{2}}{1-R}\right)^{2}}$$
Интенсивность отражённой волны найдём из закона сохранения энергии (при отсутствии поглощения и рассеяния):
$$I_{R}=I_{0}-I_{D}=\frac{4I_{0}R\sin^{2}\frac{\varphi}{2}}{\left(1-R\right)^{2}+4R\sin^{2}\frac{\varphi}{2}}$$
Кольца Ньютона
Найти радиусы интерференционных колец (колец Ньютона) в проходящем (а) и отраженном (б) свете на воздушном клине между зеркалом и плосковыпуклой линзой (её радиус $R \gg h$ — толщины линзы). Длина волны — $\lambda .$
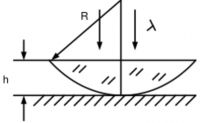
Разность хода между лучом прошедшим и лучом дважды отразившимся
и прошедшим потом равна $\Delta=2\delta$, где $\delta$ показана
на рисунке:
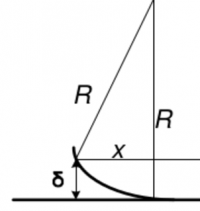
По теореме Пифагора находим $$\left(R-\delta\right)^{2}+x^{2}=R^{2},$$ тогда с учётом $x\ll R$ и следовательно $\delta^{2}\ll x^{2}$ получим $$\delta=\frac{x^{2}}{2R} \text{ и тогда разность хода } \Delta=\frac{x^{2}}{R}.$$
Условие для светлых колец: $\Delta=m\lambda,$
тёмных: $\Delta=m\lambda-\frac{1}{2}\lambda.$
Тогда радиус светлого кольца $$r_{m}=\sqrt{m\lambda R},$$ а радиус тёмного — $$r_{m}=\sqrt{\left(m-\frac{1}{2}\right)\lambda R}$$
б) Картина в проходящем свете будет дополнительной по отношению к картине в отраженном свете потому, что в зазоре происходит нечетное число отражений и фаза сдвигается еще на $\frac{1}{2}\lambda$.
Дифракция, принцип Гюйгенса.
Дифракция — явление отклонения волн от прямолинейного распространения, если только это не вызвано законами геометрической оптики (отражением, преломлением, рефракцией).
Дифракция, в частности, приводит к огибанию световыми волнами препятствий и проникновению света в область геометрической тени.
Чем сильнее ограничены поперечные размеры оптических элементов, тем сильнее проявляется дифракция.
Принцип Гюйгенса-Френеля состоит из двух положений:
1. Каждая малая по сравнению с длиной волны площадка поверхности волнового фронта может рассматриваться как источник вторичных сферических волн.
Фронт волны в последующие моменты времени представляет собой огибающую фронтов волн этих источников.
2. Вторичные волны интерферируют между собой, т.е. результирующее поле в любой точке пространства есть векторная сумма полей, создаваемых этими вторичными источниками.
Дифракционная расходимость пучка.
Пусть лазер с длиной волны $\lambda = 500$ нм светит с Земли на Луну. Каков будет минимальный размер пятна на Луне, если начальный размер лазерного пятна равен $d=1$ см?
Характерный угол дифракционной расходимости можно найти из соотношения неопределённости $$ \Delta k_{\bot} \Delta \ell \geq 2\pi . $$
В нашем случае $\Delta \ell = d$, тогда $\Delta k_{\bot} \sim \frac{2\pi}{d}$.
Тогда угол расходимости
$$\theta = \frac{\Delta k_{\bot}}{k}=\frac \lambda d.$$
Тогда радиус пятна на Луне $$ r\sim d+L\cdot 2\theta =d+\frac{2L\lambda }{d} $$
Осталось подставить значения:
$$ r\approx \frac{2\cdot 400 \cdot 10^6 \text{ м } \cdot 500 \cdot 10^{-9}\text{ м} }{10^{-2} \text{ м}}= 40 \text{ км}. $$